FlingOS™

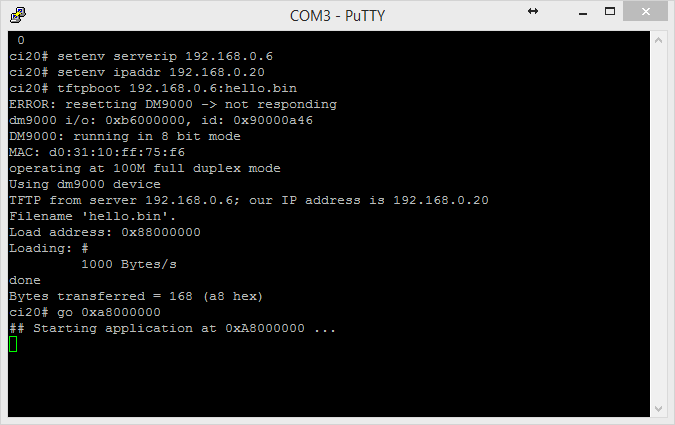
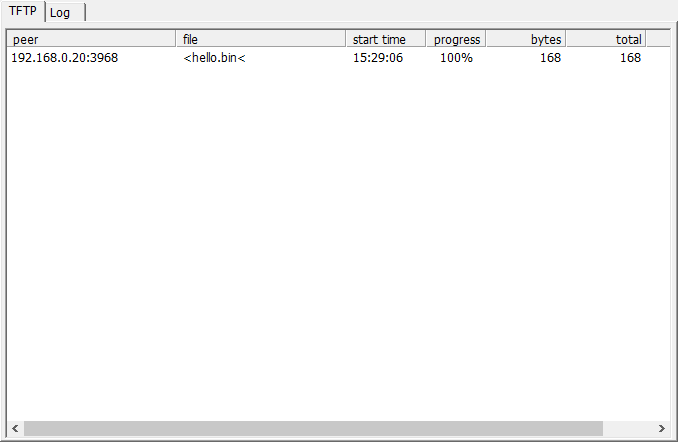
Last week, I published a post discussing how to left shift 64-bit values using the available 32-bit sized registers on MIPS. This week, we thought I should do something similar which is to provide you with another article that describes a technique that solves another interesting problem. This time I will discuss how to add two 64-bit values. This may not seem difficult at first, however we must remember that MIPS processors do not have carry flags. We need the carry flag (or something equivalent) to preserve the result of an intermediate computational step. What we have to do is somehow simulate ‘Add with carry’ without the carry to allow for the addition of 64-bit integers using 32-bit registers.

Adding two 32-bit values is trivial since the operands and the result can be contained in single registers, so here we can just use a simple ‘add’ instruction, therefore carry is not needed. The sizes of the operands for the addition instruction are either 32 or 64 bits but in order to perform the addition, the sizes must match. An exception should be raised if the sizes are not the same. Before I discuss the method for adding two 64-bit values, let’s remind ourselves how signed and unsigned values are represented in 32-bit binary. The sign extension does not have an effect on the result of the computation due to the way two’s complement works, I only include it for completeness.

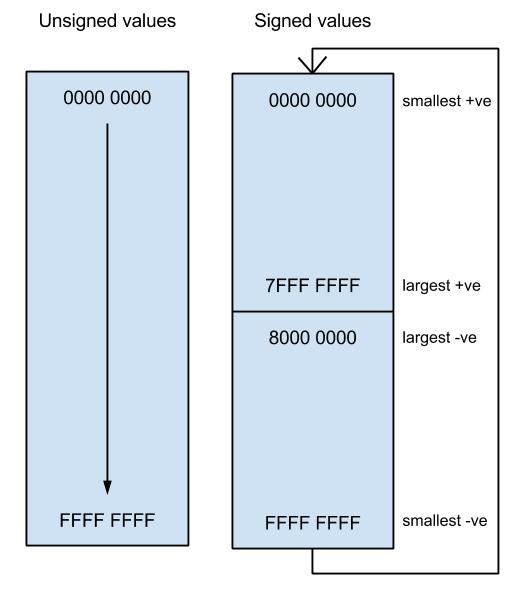
In the case of the unsigned values, the number of possible integer values goes from 0 to 2³² and they are all positive, however if we want to represent signed integers in 32 bits then we need to use one bit, the most significant bit, to represent the sign, so we can represent both positive and negative integers in the range from 0 to 2³¹. A negative value is derived such that you take a positive integer then you apply the method of two’s complement to it. Let’s see an example how to convert a positive number to its negative equivalent in 8-bit binary representation.

Two’s complement:

0000 1010   # = 10
1111 0101   # invert bits
0000 0001   # add 1
1111 0110   # = -10

First you take the integer as a bit string then you invert all the bits and finally you add one to the result. Two’s complement can also be used to convert a negative integer to positive.

Adding 64-bit operands

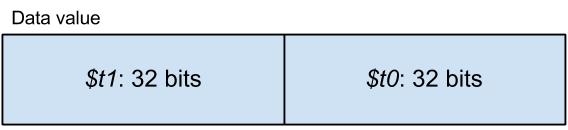
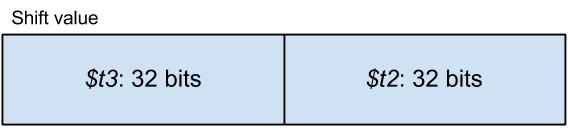
The two 64-bit integer operands have to be stored in two registers each. The first operand is stored as $t1:$t0, while the second operand is loaded as $t3:$t2.

1.      Add low bytes

The first step of this algorithm is to add the two low bytes into $t4 which we will use as a temporary storage for this partial sum.

addu $t4, $t0, $t2

We use the unsigned operation because the low-bytes do not have a sign-bit as the upper bit! We also need a way to know if there is a carry from this partial calculation. For example if we add the following two binary numbers we get a result that cannot be represented in a single register (here I assume that the registers are 4 bits in size), i.e. there is a carry bit.

1111 + 0001 = 10000

What we can do here is to store the carry bit (the 5^th bit if you like) in a temporary register in the next step.

2.      Simulate the carry flag

At this point we are going to use the ‘sltu’ instruction to store the carry bit in $t5.

sltu $t5, $t4, $t0

(Alternatively: sltu $t5, $t4, $t2 : either will do)

Here the ‘sltu’ instruction compares $t4 (sum of low bytes) with either of the individual set of low bytes ($t0 or $t2). The computation generated by the ‘sltu’ instruction goes like this. If $t4 < $t0 or if $t4 < $t2 then $t5 = 1, else $t5 = 0. It does not actually matter which set of low bytes we are using for the comparison because $t4 will always be smaller than any of the individual low bytes if there is a carry. But let me show you with some examples:

1. $t0  =  0000
   $t2  =  0000
   $t4  =  0000       $t4 = $t0 = $t2         -> $t5 = 0

Here the computation does not generate a carry. We can see that $t5 has been set to 0 as required since $t4 is not less than either $t0 or $t2.

2. $t0  =  0000
   $t2  =  1111
   $t4  =  1111       $t4 > $t0, $t4 = $t2    -> $t5 = 0

There isn’t any carry in this example either because $t4 is not less than either $t0 or $t2.

3. $t0  =  0011
   $t2  =  0110
   $t4  =  1001       $t4 > $t0, $t4 > $t2    -> $t5 = 0

No carry because $t4 is not less than $t0 or $t2.

4. $t0  =     0001
   $t2  =     1111
   $t4  =(1)0000       $t4 < $t0, $t4 < $t2    -> $t5 = 1

Now, in this example we do generate a carry, so let’s see if the method works. Remembering that $t4 is (for these examples) 4-bits in size, so the 5-th bit (the ‘1’) is lost: $t4 = 0000 because the carry bit is lost so, so $t4 < $t0 and $t4 < $t2 therefore $t5 is set to 1.

5. $t0  =  1111
   $t2  =  1111
   $t4  =(1)1110       $t4 < $t0, $t4 < $t2    -> $t5 = 1

The last example works for the same reason as the previous one did.

Using my diagram above to visualise how numbers work, it is possible to see that no two numbers added together can ever wrap round over themselves, so the result will only ever be greater than either of the operands if there was no carry. The number system forms a cycle.

3.      Add high bytes with carry

Now, we need to add the two high bytes ($t1 and $t3) plus any carry that is left from the addition of the low bytes and store the result in $t1.

addu $t5, $t5, $t1      # $t5 = carry + $t1(high bytes of operand 1)
addu $t1, $t5, $t3      # $t1 = $t5 + $t3(high bytes of operand 2)

Finally we move the sum of the low bytes into $t0.
move $t0, $t4           # move partial sum to $t0

At the end of the process we have a result as a 64-bit value stored as $t1:$t0.

I hope you found this article helpful. See you soon…

Roland

 

Yesterday, while working on the implementation of the left shift IL operation (shl) for MIPS, we came across some challenges related to shifting 64-bit values using 32-bit registers. The solution is a bit tricky, so we thought it would be useful if I produced an article discussing how it can be done.

In order to shift a string of bits, we need two operands; the data itself and a value specifying the distance we want the data to be shifted. The shift value can either be a constant or a value stored in a register. Although in this article we assume that the values are in registers, the same technique can be adapted to be used with the assembly instructions that use constant values. There are four different cases we need to consider in terms of operand sizes:

• 4-byte data, 4-byte shift value,
• 4-byte data, 8-byte shift value (this is unsupported by C#),
• 8-byte data, 4-byte shift value,
• 8-byte data, 8-byte shift value.

The 4-8 case is unsupported by C#, so in this scenario the compiler throws an exception. The 4-4 case uses a single left shift assembly instruction (sllv) so there isn’t much explanation needed there.

8 – 4 case

In the 8-4 case, the 8-byte sized data is shifted by a value that is represented by a 4-byte binary number. Since we only have 32-bit (4-byte) registers, we need to store the data in two separate registers. One register contains the low bytes ($t0) while the other contains the high bytes ($t1). In this example, I store the shift value in $t2.

Consider a 1-byte left shift, i.e. $t2 contains the value of 8. Now we have a problem because the top byte of $t0 must replace the bottom byte of $t1 as well as the rest of the data must be shifted correctly. So how do we shift an 8-byte value using 4-byte registers? I will show you how by going through some examples. There are two variations of the 8-4 case; one where $t2 < 32 and another where $t2 >= 32.

The method ($t2 < 32)

Let’s say we want to left shift this data by 1 byte (1 byte can be represented by two hexadecimal digits):

Somehow we want the result to end up looking like this:

1.      Left shift high bytes by $t2

First, we want to left shift the high 4 bytes ($t1) of the original data by the value carried by $t2, which is 1-byte. The low 4 bytes remain unchanged for now. So we have:

2.      Right shift low bytes by (32 – $t2) into temporary

The next step is to logical right shift (not arithmetic right shift!) $t0 by (32 – $t2) into a register which we will use as a temporary storage, say $t4. Since $t2’s value in bits is 8, we right shift $t0 by 24 into $t4. This way we get the proportion of $t0 which we then want to copy into $t1. $t0 and $t1 remain unchanged at this point.

 

3.      OR temporary with high bytes

Here we can combine $t1 and $t4 using the logical OR operation to get the correct result for the high 4 bytes which we store back to $t1.

 

4.      Left shift low bytes by $t2

There is only one thing to do, left shifting the low 4 bytes ($t0) by $t2.

 

Now the algorithm is complete. If we compare this result with the desired result above, we can see that they are identical.

The method ($t2 >= 32)

If $t2 >= 32 then we are left shifting the data by 32 or more bits which means that the least significant bit (little endian) of the data is pushed beyond the low bytes into the high bytes. In all cases where the shift value is greater than or equal to 32, $t0 ends up filled with zeros and the content of $t1 are lost completely. But in what form does $t0 take over $t1? Let me show you step-by-step as before. Now let’s assume that we are left shifting by 40 bits and we have the same original data as before.

 

But this time we want the result to be this:

 

1.      Move low bytes into high bytes

We copy the contents of the low bytes into the high bytes. We do this to save the contents of $t0 into $t1. The original data becomes:

 

2.      Fill low bytes with zeros

Since the data is pushed all the way beyond the low bytes, we can fill the $t0 with zeros.

 

3.      Left shift high bytes by ($t2 – 32)

The final step is to left shift $t1 by ($t2 – 32) which is 8 in our case. So the desired result is achieved as expected.

 8 – 8 case

In the 8-8 case, both the data and the shift values are 8 bytes in size. There is one important observation we must make; shifting a 64-bit value by 64 bits or more is pointless since the result will always be zero. We also know that the number 64 is represented by this binary number: 0b0100 0000 which can easily be contained in the low bytes of the shift value ($t2). Actually any non-zero value beyond the 6^th bit would yield a zero result but let’s just consider 4 bytes to be the smallest size we can manage.

  

To conclude, if $t3 is non-zero then the result of the left shift will definitely be zero, while if $t3 is zero then we can proceed the same way as in the 8-4 case by simply ignoring $t3.

I hope you found this article helpful. Please leave a comment if you think I missed something or if you have anything to add and I will do my best to respond.

See you around.

Roland