Last week, I published a post discussing how to left shift 64-bit values using the available 32-bit sized registers on MIPS. This week, we thought I should do something similar which is to provide you with another article that describes a technique that solves another interesting problem. This time I will discuss how to add two 64-bit values. This may not seem difficult at first, however we must remember that MIPS processors do not have carry flags. We need the carry flag (or something equivalent) to preserve the result of an intermediate computational step. What we have to do is somehow simulate ‘Add with carry’ without the carry to allow for the addition of 64-bit integers using 32-bit registers.
Adding two 32-bit values is trivial since the operands and the result can be contained in single registers, so here we can just use a simple ‘add’ instruction, therefore carry is not needed. The sizes of the operands for the addition instruction are either 32 or 64 bits but in order to perform the addition, the sizes must match. An exception should be raised if the sizes are not the same. Before I discuss the method for adding two 64-bit values, let’s remind ourselves how signed and unsigned values are represented in 32-bit binary. The sign extension does not have an effect on the result of the computation due to the way two’s complement works, I only include it for completeness.
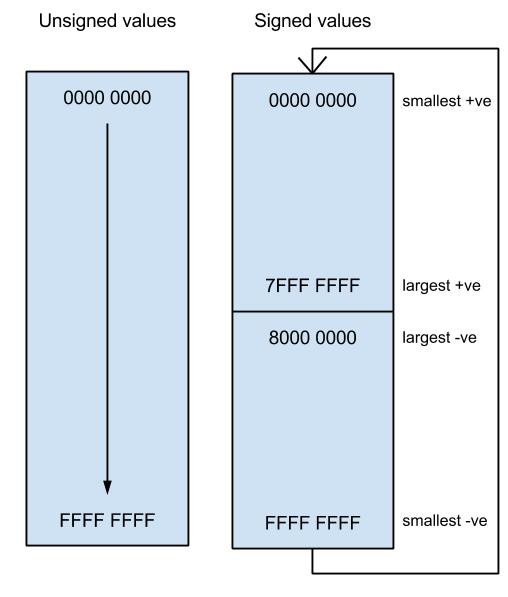
In the case of the unsigned values, the number of possible integer values goes from 0 to 232 and they are all positive, however if we want to represent signed integers in 32 bits then we need to use one bit, the most significant bit, to represent the sign, so we can represent both positive and negative integers in the range from 0 to 231. A negative value is derived such that you take a positive integer then you apply the method of two’s complement to it. Let’s see an example how to convert a positive number to its negative equivalent in 8-bit binary representation.
Two’s complement:
0000 1010 # = 10
1111 0101 # invert bits
0000 0001 # add 1
1111 0110 # = -10
First you take the integer as a bit string then you invert all the bits and finally you add one to the result. Two’s complement can also be used to convert a negative integer to positive.
Adding 64-bit operands
The two 64-bit integer operands have to be stored in two registers each. The first operand is stored as $t1:$t0, while the second operand is loaded as $t3:$t2.
1. Add low bytes
The first step of this algorithm is to add the two low bytes into $t4 which we will use as a temporary storage for this partial sum.
addu $t4, $t0, $t2
We use the unsigned operation because the low-bytes do not have a sign-bit as the upper bit! We also need a way to know if there is a carry from this partial calculation. For example if we add the following two binary numbers we get a result that cannot be represented in a single register (here I assume that the registers are 4 bits in size), i.e. there is a carry bit.
1111 + 0001 = 10000
What we can do here is to store the carry bit (the 5th bit if you like) in a temporary register in the next step.
2. Simulate the carry flag
At this point we are going to use the ‘sltu’ instruction to store the carry bit in $t5.
sltu $t5, $t4, $t0
(Alternatively: sltu $t5, $t4, $t2 : either will do)
Here the ‘sltu’ instruction compares $t4 (sum of low bytes) with either of the individual set of low bytes ($t0 or $t2). The computation generated by the ‘sltu’ instruction goes like this. If $t4 < $t0 or if $t4 < $t2 then $t5 = 1, else $t5 = 0. It does not actually matter which set of low bytes we are using for the comparison because $t4 will always be smaller than any of the individual low bytes if there is a carry. But let me show you with some examples:
- $t0 = 0000
$t2 = 0000
$t4 = 0000 $t4 = $t0 = $t2 -> $t5 = 0
Here the computation does not generate a carry. We can see that $t5 has been set to 0 as required since $t4 is not less than either $t0 or $t2.
- $t0 = 0000
$t2 = 1111
$t4 = 1111 $t4 > $t0, $t4 = $t2 -> $t5 = 0
There isn’t any carry in this example either because $t4 is not less than either $t0 or $t2.
- $t0 = 0011
$t2 = 0110
$t4 = 1001 $t4 > $t0, $t4 > $t2 -> $t5 = 0
No carry because $t4 is not less than $t0 or $t2.
- $t0 = 0001
$t2 = 1111
$t4 =(1)0000 $t4 < $t0, $t4 < $t2 -> $t5 = 1
Now, in this example we do generate a carry, so let’s see if the method works. Remembering that $t4 is (for these examples) 4-bits in size, so the 5-th bit (the ‘1’) is lost: $t4 = 0000 because the carry bit is lost so, so $t4 < $t0 and $t4 < $t2 therefore $t5 is set to 1.
- $t0 = 1111
$t2 = 1111
$t4 =(1)1110 $t4 < $t0, $t4 < $t2 -> $t5 = 1
The last example works for the same reason as the previous one did.
Using my diagram above to visualise how numbers work, it is possible to see that no two numbers added together can ever wrap round over themselves, so the result will only ever be greater than either of the operands if there was no carry. The number system forms a cycle.
3. Add high bytes with carry
Now, we need to add the two high bytes ($t1 and $t3) plus any carry that is left from the addition of the low bytes and store the result in $t1.
addu $t5, $t5, $t1 # $t5 = carry + $t1(high bytes of operand 1)
addu $t1, $t5, $t3 # $t1 = $t5 + $t3(high bytes of operand 2)
Finally we move the sum of the low bytes into $t0.
move $t0, $t4 # move partial sum to $t0
At the end of the process we have a result as a 64-bit value stored as $t1:$t0.
I hope you found this article helpful. See you soon…
Roland