Yesterday, while working on the implementation of the left shift IL operation (shl) for MIPS, we came across some challenges related to shifting 64-bit values using 32-bit registers. The solution is a bit tricky, so we thought it would be useful if I produced an article discussing how it can be done.
In order to shift a string of bits, we need two operands; the data itself and a value specifying the distance we want the data to be shifted. The shift value can either be a constant or a value stored in a register. Although in this article we assume that the values are in registers, the same technique can be adapted to be used with the assembly instructions that use constant values. There are four different cases we need to consider in terms of operand sizes:
- 4-byte data, 4-byte shift value,
- 4-byte data, 8-byte shift value (this is unsupported by C#),
- 8-byte data, 4-byte shift value,
- 8-byte data, 8-byte shift value.
The 4-8 case is unsupported by C#, so in this scenario the compiler throws an exception. The 4-4 case uses a single left shift assembly instruction (sllv) so there isn’t much explanation needed there.
8 – 4 case
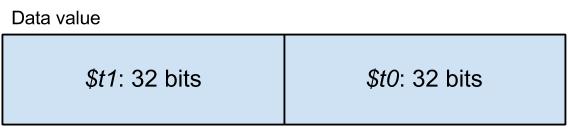
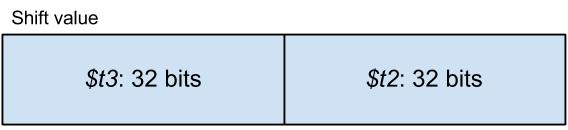
In the 8-4 case, the 8-byte sized data is shifted by a value that is represented by a 4-byte binary number. Since we only have 32-bit (4-byte) registers, we need to store the data in two separate registers. One register contains the low bytes ($t0) while the other contains the high bytes ($t1). In this example, I store the shift value in $t2.
Consider a 1-byte left shift, i.e. $t2 contains the value of 8. Now we have a problem because the top byte of $t0 must replace the bottom byte of $t1 as well as the rest of the data must be shifted correctly. So how do we shift an 8-byte value using 4-byte registers? I will show you how by going through some examples. There are two variations of the 8-4 case; one where $t2 < 32 and another where $t2 >= 32.
The method ($t2 < 32)
Let’s say we want to left shift this data by 1 byte (1 byte can be represented by two hexadecimal digits):
Somehow we want the result to end up looking like this:
1. Left shift high bytes by $t2
First, we want to left shift the high 4 bytes ($t1) of the original data by the value carried by $t2, which is 1-byte. The low 4 bytes remain unchanged for now. So we have:
2. Right shift low bytes by (32 – $t2) into temporary
The next step is to logical right shift (not arithmetic right shift!) $t0 by (32 – $t2) into a register which we will use as a temporary storage, say $t4. Since $t2’s value in bits is 8, we right shift $t0 by 24 into $t4. This way we get the proportion of $t0 which we then want to copy into $t1. $t0 and $t1 remain unchanged at this point.
3. OR temporary with high bytes
Here we can combine $t1 and $t4 using the logical OR operation to get the correct result for the high 4 bytes which we store back to $t1.
4. Left shift low bytes by $t2
There is only one thing to do, left shifting the low 4 bytes ($t0) by $t2.
Now the algorithm is complete. If we compare this result with the desired result above, we can see that they are identical.
The method ($t2 >= 32)
If $t2 >= 32 then we are left shifting the data by 32 or more bits which means that the least significant bit (little endian) of the data is pushed beyond the low bytes into the high bytes. In all cases where the shift value is greater than or equal to 32, $t0 ends up filled with zeros and the content of $t1 are lost completely. But in what form does $t0 take over $t1? Let me show you step-by-step as before. Now let’s assume that we are left shifting by 40 bits and we have the same original data as before.
But this time we want the result to be this:
1. Move low bytes into high bytes
We copy the contents of the low bytes into the high bytes. We do this to save the contents of $t0 into $t1. The original data becomes:
2. Fill low bytes with zeros
Since the data is pushed all the way beyond the low bytes, we can fill the $t0 with zeros.
3. Left shift high bytes by ($t2 – 32)
The final step is to left shift $t1 by ($t2 – 32) which is 8 in our case. So the desired result is achieved as expected.
8 – 8 case
In the 8-8 case, both the data and the shift values are 8 bytes in size. There is one important observation we must make; shifting a 64-bit value by 64 bits or more is pointless since the result will always be zero. We also know that the number 64 is represented by this binary number: 0b0100 0000 which can easily be contained in the low bytes of the shift value ($t2). Actually any non-zero value beyond the 6th bit would yield a zero result but let’s just consider 4 bytes to be the smallest size we can manage.
To conclude, if $t3 is non-zero then the result of the left shift will definitely be zero, while if $t3 is zero then we can proceed the same way as in the 8-4 case by simply ignoring $t3.
I hope you found this article helpful. Please leave a comment if you think I missed something or if you have anything to add and I will do my best to respond.
See you around.
Roland












One thought on “Left shifting 64-bit values using 32-bit registers”